
法国纪录片《维度:数学漫步 Dimensions: A Walk Through Mathematics 2008》介绍
法国纪录片《维度:数学漫步 Dimensions: A Walk Through Mathematics 2008》以英语中字呈现,采用 MKV 格式,文件大小 1.27GB,是一部时长两小时的数学 CG 科普佳作。这部纪录片打破了 “数学 = 枯燥公式” 的刻板印象,以 “可视化” 为核心手段,借助精湛的计算机图形技术(CG),将 4 维空间中的正多胞体、复数、分形、纤维化理论等深奥数学知识,转化为直观可感的动态影像,让观众在 “漫步数学世界” 的过程中,感受抽象理论背后的逻辑之美与宇宙规律,兼具专业性、趣味性与审美价值。
对于多数人而言,“4 维空间”“分形” 等概念如同 “天书”,仅靠文字描述难以理解。而这部纪录片的突破之处,在于用 CG 技术搭建起 “抽象概念与现实感知” 的桥梁。以 “4 维空间中的正多胞体” 为例,人类身处 3 维空间,无法直接观测 4 维物体,纪录片便通过 “维度类比” 的方式逐步引导:先从 1 维线段、2 维正方形、3 维立方体的构造逻辑入手,展示 “低维物体如何通过‘延伸’生成高维物体”——1 维线段沿垂直方向延伸形成 2 维正方形,2 维正方形沿垂直方向延伸形成 3 维立方体,以此类推,推导出 “3 维立方体沿第 4 个维度延伸可生成 4 维正多胞体(如超立方体)”。随后,通过 CG 动画将超立方体 “投影” 到 3 维空间,展示其在旋转过程中 “面与面的重叠、形态的动态变化”,让观众直观理解 4 维物体的结构特征,而非单纯记忆抽象定义。
“复数” 这一概念的呈现,同样体现了纪录片的巧思。复数由实数与虚数组成,其运算规则与几何意义是学习难点。纪录片没有直接抛出公式,而是从 “实数与数轴” 的对应关系切入,通过 CG 动画构建 “复平面”—— 将实数轴作为横轴,虚数轴作为纵轴,复数便对应复平面上的一个点。在讲解复数乘法时,动画将 “乘以虚数 i” 转化为 “点在复平面上逆时针旋转 90 度”,将 “模长相乘、辐角相加” 的运算规则,转化为 “点的位置缩放与旋转” 的几何运动,让抽象的代数运算变成可观察的图形变化。这种 “代数与几何结合” 的可视化方式,不仅降低了理解门槛,更让观众体会到数学中 “数与形” 的内在统一。
“分形” 作为数学中的 “艺术符号”,是纪录片的视觉亮点之一。分形具有 “自相似性”—— 整体与局部在形态上高度相似,无论放大多少倍,都能看到与整体相似的细节。纪录片通过 CG 动画生成经典分形图形(如曼德博集合、科赫雪花):从一个简单的三角形开始,每一次迭代都在每条边上生成更小的三角形,最终形成边缘无限复杂、周长无限长但面积有限的科赫雪花;而曼德博集合则通过复数迭代生成,其边缘的 “褶皱” 中隐藏着无数与整体相似的微小结构,动画通过 “不断放大局部” 的镜头,让观众惊叹于分形图形的无限细节与对称美感。同时,纪录片还将分形与自然现象(如树枝分叉、云朵边缘、海岸线形态)结合,指出分形理论正是对自然规律的数学抽象,让观众意识到 “深奥数学其实藏在日常生活中”。
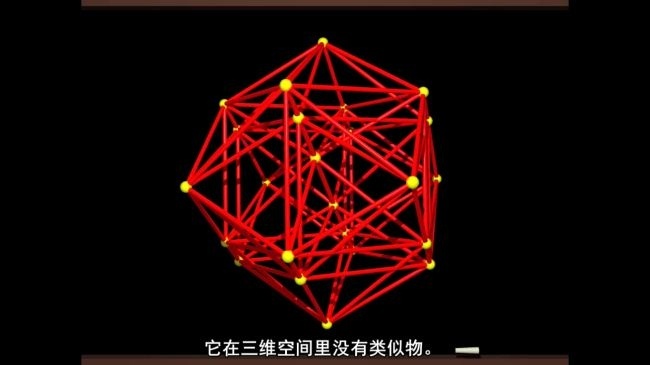
“纤维化理论” 作为相对高深的数学分支,纪录片通过 “类比现实场景” 的方式降低理解难度。纤维化理论可简单理解为 “将一个空间‘分解’为多个相似的子空间,且这些子空间通过某种规则连接”。纪录片用 CG 动画构建 “圆柱面纤维化” 模型:将圆柱面看作 “无数与轴线平行的直线(纤维)” 组成,这些直线通过 “圆周(底空间)” 连接,形成完整的圆柱面;再延伸至更复杂的 “环面纤维化”,展示不同纤维化方式如何生成不同的空间结构。这种 “从简单到复杂” 的演示,让观众逐步理解纤维化理论中 “整体与局部的关系”,感受数学对空间结构的精妙描述。
整部纪录片的制作风格兼具 “科学性与艺术性”:CG 画面色彩柔和、细节精致,既确保数学概念的准确呈现,又具有视觉冲击力;旁白讲解语言通俗,避免堆砌专业术语,注重 “逻辑递进”—— 从基础概念铺垫,到核心理论解析,再到现实应用关联,层层递进引导观众思考。1.27GB 的文件体量,既保证了 CG 画面的清晰度,又便于传播与观看。

无论是对数学感兴趣的学生、教育工作者,还是对 “数学之美” 好奇的普通观众,都能从这部纪录片中获得启发。它不仅是一部科普作品,更是一次 “数学审美之旅”—— 让观众看到,数学不是枯燥的公式与计算,而是探索宇宙规律、描述空间形态、连接艺术与自然的 “语言”,真正实现了 “让深奥数学走进大众” 的科普目标。
